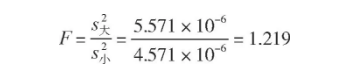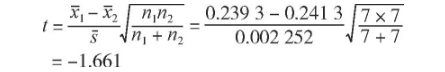如何判斷標準樣品的值是否發生了變化(實例講解)
2018-08-28
作者:
瀏覽數:1656
標準物質能夠在時間和空間上傳遞量值, 從而建立了測量的量值溯源性, 同時也保證了測量的量值可比性, 因此在各行各業的理化實驗室有著非常廣泛的應用。根據管理要求, 實驗室應在技術條件允許的情況下, 對使用中的標準物質進行核查。
標準物質的量值是其研制機構按照規定的要求, 通過一系列的實驗和統計, 經評審后確定并發布的。關于標準物質的核查, 有很多討論, 但有一點毋庸置疑:使用中標準物質的量值應在可能的條件下予以充分關注。
雖然核查使用中標準物質的量值需要非常高的技術要求, 但實驗室可以從標準物質的具體使用條件出發, 利用已有的儀器進行測試, 通過統計檢驗, 判斷使用中標準物質的量值與新購標準物質的量值是否存在顯著性差異。因為是兩個量值之間的比較, t檢驗法是最適合的, 其基本步驟是:計算統計量t的絕對值, 查表得相應的臨界值, 如果計算值小于臨界值, 可認為兩者沒有顯著性差異, 反之則反。
1 相同目標值的t檢驗法
多數儀器分析方法都需要將溶液標準物質稀釋成系列濃度的標準溶液, 并利用該系列標準溶液獲得工作曲線后, 再進行待測樣品的測試, 如原子吸收分光光度法、離子色譜法等。在測試的對象、方法和儀器不改變的前提下, 系列標準溶液的濃度是固定的。以原子吸收分光光度法測銅元素所需的銅標準溶液為例, 詳細介紹相同目標值的t檢驗法。
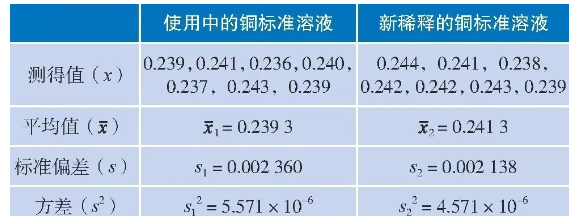
將某編號的國家二級標準物質水中銅1 000 mg/L, 按實驗室制訂的作業指導書規定的步驟稀釋至2.00 mg/L銅標準溶液, 正常使用一段時間后, 再次采購該編號的國家二級標準物質, 同樣按作業指導書規定的步驟稀釋至2.00 mg/L銅標準溶液, 即前后兩次稀釋的目標值相同。
在原子吸收分光光度計正常工作條件下, 分別重復測試使用中的和新稀釋的2.00 mg/L銅標準溶液的吸光度各7次, 分別求出兩組數據的平均值、標準偏差和方差, 數據匯總見表1。
表1 使用中的和新稀釋的2.00 mg/L銅標準溶液的吸光度
t檢驗應用的前提是兩組數據的標準偏差沒有顯著性差異, 即兩組數據是等精度的。根據F檢驗的計算公式得
取95%置信概率, 則α=0.05;又兩組數據的測量次數均為7次, 即n1=n2=7, 則f1=f2=7-1=6。查表得Fα, f1, f2=F0.05, 6, 6=4.28, 則F
最后根據公式計算統計量t, 得
因為僅檢驗兩個平均值是否不同, 不關心孰大孰小, 故為雙尾檢驗 (也叫雙側檢驗) 。取α=0.05, 查表得tα, n1+n2-2=t0.005, 12=2.18。因為|t|
通常情況下, 凡是由高濃度溶液標準物質稀釋至特定濃度標準溶液的, 都可以用上述方法檢驗使用中標準物質的量值與新稀釋標準物質的量值是否存在顯著性差異。
2 不同目標值的t檢驗法
有些儀器分析方法所用的標準物質是固態的、直接使用的, 不能像前文所述的溶液標準物質那樣稀釋至任意指定的目標濃度, 如直讀光譜儀標準物質、紅外碳硫分析儀標準物質。與多數溶液標準物質不同, 這些固態標準物質在制備過程中無法精準控制其特征量值, 即使是同一標準物質編號, 不同批次的量值也會在一定范圍內波動。以直讀光譜儀測試所用的低合金鋼標準物質中的錳元素為例, 詳細介紹不同目標值的t檢驗法。
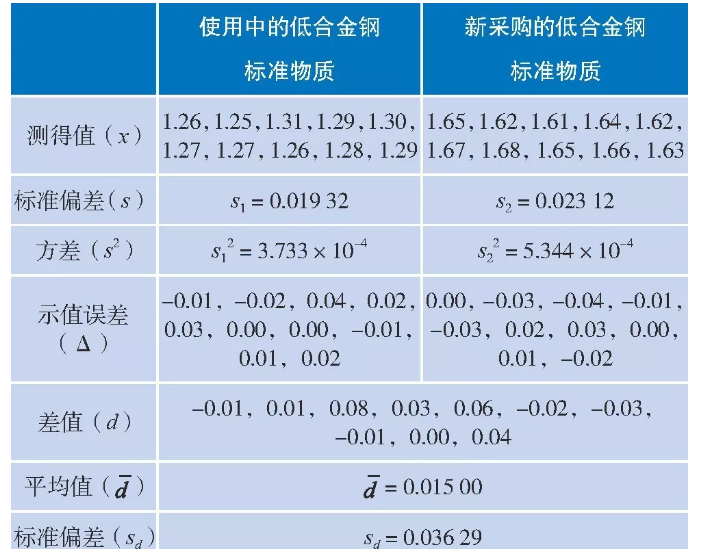
某低合金鋼標準物質中錳元素質量分數的標準值為1.27%, 按操作規范正常使用一段時間后, 再次采購低合金鋼標準物質 (可以是不同的標準物質編號, 但兩者錳元素的質量分數應盡可能接近) , 其錳元素質量分數的標準值為1.65%。兩者錳元素質量分數的標準值存在差異, 是兩個不同的目標值, 可以用“對子分析”的方法進行t檢驗。
在直讀光譜儀正常工作條件下, 分別重復測試使用中的和新采購的低合金鋼標準物質中錳元素的質量分數各10次, 分別求出兩組數據的標準偏差和方差, 數據匯總見表2。
對兩組數據進行F檢驗, 以判斷是否等精度。根據F檢驗的計算公式得
取95%置信概率, α=0.05。查表得F0.05, 9, 9=3.18, F
表2 使用中和新采購的低合金鋼標準物質中錳元素的質量分數(%)
下一步, 分別計算兩組測試值與其標準值的差值, 可得到兩組示值誤差, 構成十對“對子”;然后計算每對對子的差值, 新得到一組十個數的數據;再計算該組差值的平均值和標準偏差。上述數據已列于表2。
最后根據公式計算統計量t, 得,
同樣僅檢驗兩個平均值是否不同, 故為雙尾檢驗。查表得t0.05, 9=2.26。因為|t|
“對子分析”可用于比較在不同實驗條件下的實驗結果, 是平均數比較的一個特例。用直讀光譜儀測試低合金鋼標準物質中錳元素的質量分數, 其實也就是用低合金鋼標準物質測試直讀光譜儀錳元素的示值誤差。當用兩種錳元素含量接近的低合金鋼標準物質測試同一臺直讀光譜儀的示值誤差時, 在儀器正常的情況下, 只要測試次數足夠多, 所得的結果不應有顯著性差異。因此, 用“對子分析”的方法檢驗使用中直讀光譜儀標準物質的方法是合理的。
通常情況下, 基體標準物質在研制及復制時, 能夠對其準確定值, 但不能精準地控制其量值。對于此類標準物質, 可以用“對子分析”的方法獲得統計量t, 以檢驗兩組數據是否存在顯著性差異。
以上兩個例子中, 無論是F檢驗還是t檢驗, 兩組數據都不存在顯著性差異。兩組數據是由同一臺儀器測得的, 在儀器和標準物質都正常的情況下, 只要測試次數足夠多, 理論上這兩組數據必然是等精度的。如果在F檢驗時發現兩組數據的方差存在顯著性差異, 在排除儀器異常的前提下, 可適當增加測試次數。如果增加測試次數后, 兩組數據仍然不是等精度的, 就需要對標準物質作進一步檢查, 尤其是使用中的標準物質。
同樣, 如果經t檢驗發現兩組數據存在顯著性差異, 可適當增加測試次數。如果增加測試次數后, 統計量t的計算值仍大于臨界值, 需要對標準物質作進一步檢查, 重點應關注使用中的標準物質。
需要說明的是, 此方法不是用來核查標準物質量值的, 只是用統計檢驗的方法判斷使用中的標準物質與新采購的標準物質所測得的數據是否存在顯著性差異。絕大多數實驗室不具備核查標準物質量值的技術條件, 從這里也可以發現, 統計量t是基于標準物質的具體使用條件獲得的。在第一個例子中, 用原子吸收分光光度計測試, 沒有顯著性差異, 但如果改用準確度更高的庫侖分析法測試, 很可能就會有顯著性差異了。本著“符合使用要求即可”的原則, 可以認為這種檢驗方法是合理的、有效的。
需要強調的是, t檢驗不是萬無一失的。在大多數情況下, 統計量t是基于一個正常運行的分析系統的統計參數的估計值, 并且是在一定置信概率下的估計值。更重要的是, 統計量t無法識別單次測試結果是偶然發生的粗大誤差還是分析系統的短期波動。盡管如此, 用統計量t檢驗使用中標準物質的量值, 對實驗室內部質量控制是非常有幫助的。